Expression Tree Infix Prefix Postfix

Binary tree representing a mathematical expression

A binary expression tree is a specific kind of a binary tree used to represent expressions. Two common types of expressions that a binary expression tree tin represent are algebraic^[1] and boolean. These copse tin can represent expressions that comprise both unary and binary operators.^[1]

Similar any binary tree, each node of a binary expression tree has zero, 1, or two children. This restricted structure simplifies the processing of expression copse.

Overview [edit]

Expression tree of the expression (a+b)*c+7

The leaves of a binary expression tree are operands, such as constants or variable names, and the other nodes incorporate operators. These detail trees happen to be binary, because all of the operations are binary, and although this is the simplest example, it is possible for nodes to accept more 2 children. It is also possible for a node to have only one child, as is the case with the unary minus operator. An expression tree, T, can be evaluated by applying the operator at the root to the values obtained by recursively evaluating the left and right subtrees.^[2]

Traversal [edit]

An algebraic expression can be produced from a binary expression tree by recursively producing a parenthesized left expression, then printing out the operator at the root, and finally recursively producing a parenthesized right expression. This general strategy (left, node, right) is known as an in-order traversal. An alternate traversal strategy is to recursively impress out the left subtree, the right subtree, and then the operator. This traversal strategy is generally known as post-order traversal. A third strategy is to print out the operator first and then recursively print out the left and right subtree known as pre-gild traversal.^[two]

These three standard depth-first traversals are representations of the three different expression formats: infix, postfix, and prefix. An infix expression is produced by the inorder traversal, a postfix expression is produced by the post-society traversal, and a prefix expression is produced by the pre-lodge traversal.^[3]

Infix traversal [edit]

When an infix expression is printed, an opening and closing parenthesis must be added at the beginning and catastrophe of each expression. As every subtree represents a subexpression, an opening parenthesis is printed at its showtime and the closing parenthesis is printed after processing all of its children.

Pseudocode:

                        Algorithm                                    infix                                    (            tree            )                        /*Print the infix expression for an expression tree.                          Pre : tree is a arrow to an expression tree                          Post: the infix expression has been printed*/                                                if                                    (            tree                                    not                                    empty            )                                                if                                    (            tree                                    token                                    is                                    operator            )                                                print                                    (            open                                    parenthesis            )                                                end                                    if                                                infix                                    (            tree                                    left                                    subtree            )                                                impress                                    (            tree                                    token            )                                                infix                                    (            tree                                    right                                    subtree            )                                                if                                    (            tree                                    token                                    is                                    operator            )                                                print                                    (            close                                    parenthesis            )                                                finish                                    if                                                end                                    if                        end                                    infix

Postfix traversal [edit]

The postfix expression is formed by the basic postorder traversal of any binary tree. Information technology does not require parentheses.

Pseudocode:

                        Algorithm                                    postfix                                    (            tree            )                        /*Print the postfix expression for an expression tree.                          Pre : tree is a arrow to an expression tree                          Post: the postfix expression has been printed*/                                                if                                    (            tree                                    not                                    empty            )                                                postfix                                    (            tree                                    left                                    subtree            )                                                postfix                                    (            tree                                    right                                    subtree            )                                                print                                    (            tree                                    token            )                                                end                                    if                        end                                    postfix

Prefix traversal [edit]

Pseudocode:

                        Algorithm                                    prefix                                    (            tree            )                        /*Print the prefix expression for an expression tree.                          Pre : tree is a pointer to an expression tree                          Mail service: the prefix expression has been printed*/                                                if                                    (            tree                                    not                                    empty            )                                                print                                    (            tree                                    token            )                                                prefix                                    (            tree                                    left                                    subtree            )                                                prefix                                    (            tree                                    right                                    subtree            )                                                stop                                    if                        end                                    prefix

Construction of an expression tree [edit]

The construction of the tree takes identify by reading the postfix expression one symbol at a time. If the symbol is an operand, a one-node tree is created and its pointer is pushed onto a stack. If the symbol is an operator, the pointers to ii trees T1 and T2 are popped from the stack and a new tree whose root is the operator and whose left and right children indicate to T2 and T1 respectively is formed . A pointer to this new tree is so pushed to the Stack.^[iv]

Example [edit]

The input in postfix notation is: a b + c d e + * * Since the first two symbols are operands, one-node trees are created and pointers to them are pushed onto a stack. For convenience the stack will grow from left to right.

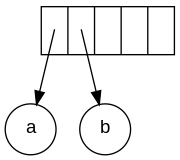
Stack growing from left to right

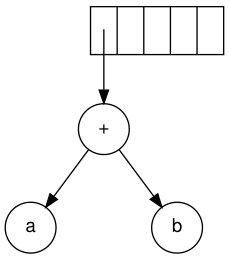
The adjacent symbol is a '+'. It pops the two pointers to the trees, a new tree is formed, and a pointer to it is pushed onto the stack.

Next, c, d, and e are read. A 1-node tree is created for each and a pointer to the corresponding tree is pushed onto the stack.

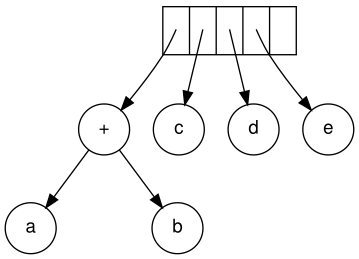
Standing, a '+' is read, and it merges the last 2 trees.

Now, a '*' is read. The last two tree pointers are popped and a new tree is formed with a '*' as the root.

Forming a new tree with a root

Finally, the last symbol is read. The two trees are merged and a pointer to the concluding tree remains on the stack.^[5]

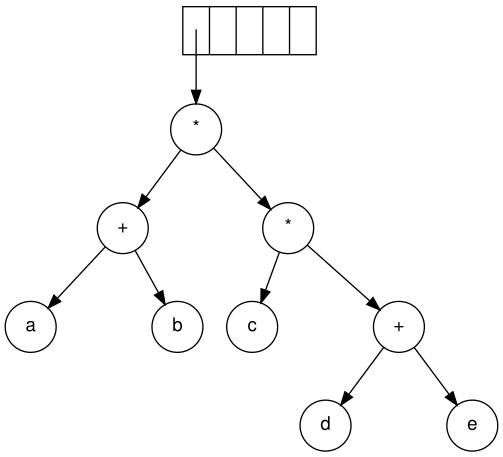
Steps to construct an expression tree a b + c d e + * *

Algebraic expressions [edit]

Binary algebraic expression tree equivalent to ((5 + z) / -8) * (iv ^ 2)

Algebraic expression trees correspond expressions that contain numbers, variables, and unary and binary operators. Some of the common operators are × (multiplication), ÷ (division), + (addition), − (subtraction), ^ (exponentiation), and - (negation). The operators are independent in the internal nodes of the tree, with the numbers and variables in the leaf nodes.^[i] The nodes of binary operators have ii child nodes, and the unary operators have one child node.

Boolean expressions [edit]

Boolean expressions are represented very similarly to algebraic expressions, the but divergence being the specific values and operators used. Boolean expressions use true and false as constant values, and the operators include $\land$ (AND), $\lor$ (OR), $\neg$ (Non).

References [edit]

^ ^a ^b ^c Bruno R. Preiss (1998). "Expression Trees". Archived from the original on January 19, 2017. Retrieved Dec xx, 2010.
^ ^a ^b Gopal, Arpita. Magnifying Data Structures. PHI Learning, 2010, p. 352.
^ Richard F. Gilberg & Behrouz A. Forouzan. Information Structures: A Pseudocode Approach with C. Thomson Form Technology, 2005, p. 280.
^ Mark Allen Weiss,Information Structures and Algorithm Analysis in C,second edition, Addison Wesley publications
^ Gopal, Arpita. Magnifying Data Structures. PHI Learning, 2010, p. 353.